데이터베이스 이론 -ER 모델
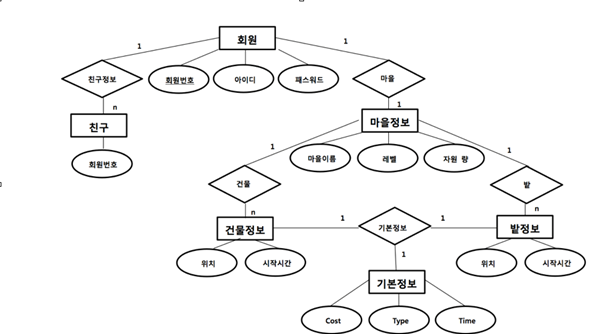
ER 모델 (Entity-Relationship model) 은 데이터베이스를 디자인하기 위해 이용되는 모델링 기법으로, 데이터베이스에 대한 요구 사항을 그래픽적으로 표현하는 방법이다. 요구사항으로부터 얻어낸 정보들을 개체(Entity), 애트리뷰트(Attribute), 관계성(Relation)으로 기술하는 데이터 모델을 말한다.
ER 모델에서는 데이터베이스에 저장되는 데이터들을 추상화하여 나타내기 때문에 특정 DBMS 및 하드웨어에 독립적으로 데이터베이스의 구조를 나타낼 수 있다.
개체( Entity )
개체란 단독으로 존재하는 객체를 의미하며, 동일한 객체는 존재하지 않는다.
예를 들어, 학생 정보가 학번, 이름, 학년이 있을 때, 3개의 정보가 모두 같은 학생이 오직 한 명이면 이를 개체라고 한다.
즉, 학생 한 명이 개체가 된다.
이 개체들의 집합을 Entity Type이라고 한다.
ER 다이어그램에서 Entity Type은 사각형으로 표현한다.
개체에는 weak entity와 regular entity가 있다.
- weak entity: 개체가 가진 속성들로는 개체를 고유하게 정의할 수 없는 개체를 말한다. 예를 들어, 학과 (department)라는 개체는 A라는 학교와 B라는 학교 모두에 존재할 수 있기 때문에 학교라는 개체와의 관계를 명시해야 학과라는 개체를 정의할 수 있다. 따라서, 학과라는 개체는 weak entity에 해당한다.
- regular entity: weak entity가 아닌 모든 개체를 말한다.
애트리뷰트, 속성( Attribute )
개체가 갖는 속성을 의미한다.
예를 들어, Student에서 학번, 이름, 학년 같은 정보를 속성이라 한다.
ER 다이어그램에서 Attribute는 원으로 표현한다.
simple attribute
더 이상 나누어지지 않는 속성을 말하며, simple attribute로는 번지, 도시 등이 있다.
composite attribute(복합 애트리뷰트): 두 개 이상의 속성으로 구성된 것을 말한다. 예를 들어, 학생의 주소를 나타내는 Address 애트리뷰트가 있을 때, 우리나라에서 주소는 "경기도", "OO시", "OO동", "OO아파트"와 같이 표현한다.
즉 Address는 위의 4개의 독립된 Attribute가 모여서 생성된 Attribute이므로 Address를 Composite Attribute라고 한다.

key attribute
객체를 유일하게 구별할 수 있는 속성으로 다른 객체들과 중복되지 않는 고유한 값을 가진 Attribute로서, 주로 객체를 식별하는데 사용된다.
예를 들어, 학생의 학번을 의미하는 Student_no는 다른 학생들과 중복되지 않는 고유한 번호다.
따라서 Student_no는 Key Attribute 입니다.
Key Attribute를 ER 다이어그램에서는 원에 밑줄로 표시한다.

single-valued attribute
하나의 객체가 하나의 값만 가질 수 있는 속성을 말한다. 사람의 성별은 single-valued attribute에 해당한다.
multi-valued attribute
하나의 객체가 여러 값을 가질 수 있는 속성을 말한다.
예를 들어, 학생의 전공을 나타내는 Degree Attribute가 있다고 있을 때, 이 학생이 복수 전공을 할 경우 Degree Attribute 값이 2개가 되므로, 이 때 Degree Attribute를 Multi-Valued Attribute라고 한다.
Multi-Valued Attribute는 ER 다이어그램에서 두 개의 원으로 표현한다.

base attribute
다른 속성으로부터 유도되지 않고, 오직 해당 속성을 참조해야만 값을 알 수 있는 속성을 말한다.
derived attribute
다른 속성으로부터 값이 결정될 수 있는 속성을 말한다. 예를 들어, 어떠한 사람의 나이는 그 사람의 주민등록번호를 참조하면 결정할 수 있기 때문에 나이는 derived attribute에 해당한다.
Derived Attribute는 ER 다이어그램에서 원을 점선으로 표현한다.

관계 ( Relation )
관계를 맺는 두 Entity Type에 대해, 한 개체가 얼마나 많은 다른 개체와 관련될 수 있는지를 나타내는 제약조건을 뜻한다.
예를 들어, 수강을 뜻하는 Takes는 학생과 과목 간의 "수강"이라는 관계를 갖는다.
이 때 Takes를 Relation Type이라 하며, Relation Type 역시 속성을 가질 수 있다.
ER 다이어그램에서 Relation은 마름모로 표현한다.
1) 카디널리티 비율 제약조건 ( Cardinality Ratio Constraint )
관계를 맺는 두 Entity Type에 대해, 한 개체가 얼마나 많은 다른 개체와 관련될 수 있는지를 나타내는 제약조건을 뜻한다.
일대일(1 : 1) : 두 개 Entity Type의 개체들은 서로 일대일로 대응.
일대다(1 : N) : 하나의 개체가 다른 Entity Type의 많은 개체들과 관련되지만, 그 역은 성립하지 않음
다대다(N : M) : 하나의 개체가 다른 Entity Type의 많은 개체들과 관련되며, 역이 성립.
예를 들어, "학사 관리 시스템"에서 한 학생은 많은 과목을 수강할 수 있고 한 과목에는 많은 학생이 수강하므로, Student Entity Type과 Course Entity Type은 N : M 관계다.

또 다른 예시로, 부모와 자식 Entity Type 관계에서 부모는 많은 자식을 가질 수 있지만 자식은 한 부모만 가질 수 있다.
즉, 부모와 자식은 1 : M 관계이며, 이를 ER 다이어그램으로 다음과 같이 표현할 수 있다.
간혹 1과 M을 어느 선에 명시해야 할지 헷갈리는 경우가 있는데, M에 해당하는 Entity Type에 M을 명시해주면 된다.

2) 참여 제약조건 ( Participation Constraint )
관계를 맺는 두 Entity Type에 대해 한 개체의 존재가 다른 개체의 존재에 의존하는지 여부를 나타내는 제약조건.
전체 참여 ( Total Participation ) : 하나 또는 그 이상의 개체가 참여
부분 참여 ( Partial Participation ) : 선택적인 참여
에를 들어, 학생은 과목을 꼭 수강 할 필요가 없지만 과목은 항상 수강생이 있어야 합니다.
수강생이 없는 과목은 폐강되기 때문이다. ER 모델에서 전체 참여는 두 개의 실선으로 부분 참여는 한 개의 실선으로 표현하고, 이를 표현하면 다음과 같다.

3) 구조적 제약조건 ( Structural Constraint )
앞서 살펴 본 두 개의 제약조건을 가리켜 구조적 제약조건이라 한다.
구조적 제약조건은 관계를 맺는 두 Entity Type에 1 , N , M을 표시하거나 한 줄 또는 두 줄을 표시하지 말고 ( MIN, MAX ) 방식으로 두 제약조건을 한 번에 표현하는 방식이다.
예를 들어, 학생은 최소 3개, 최대 6개의 강의를 수강할 수 있으며, 강의는 최소 10명 최대 100명의 학생들이 들을 수 있을 때, 이를 ER 다이어그램으로 표현하면 다음과 같다.

subtype과 supertype
모든 개체는 적어도 하나 이상의 개체 타입을 갖는다. 관계형 데이터베이스에서는 개체가 갖는 타입에 대해 subtype과 supertype라는 개념이 존재한다. 예를 들어, 직원 정보가 저장된 데이터베이스에서 Programmer에 해당하는 개체는 Employee라는 개체의 subtype이며, 반대로 Employee라는 개체는 Programmer라는 개체의 supertype에 해당한다. 이러한 subtype과 supertype 관계에 있는 개체는 다음과 같은 속성을 갖는다.
supertype에 해당하는 개체가 갖는 모든 속성은 subtype에 해당하는 개체에 적용할 수 있다. 그러나 그 반대는 항상 가능하지 않다.
subtype에 해당하는 개체는 자동적으로 supertype에 해당하는 개체가 연관된 모든 관계에 포함된다.
아래 블로그의 글을 참고해서 작성하였습니다.
'Database > 데이터베이스 이론' 카테고리의 다른 글
| [Database] ODS(Operational Data Store)란? (0) | 2020.07.29 |
|---|---|
| [UML] 유스케이스 다이어그램(Usecase Diagram) (1) | 2020.07.06 |
| [UML] 클래스 다이어그램(Class Diagram) 정리 (1) | 2020.03.26 |
![[데이터베이스 이론] ER 모델 - 개념적 모델링](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbWSZk6%2FbtqC4s69eqR%2FAAAAAAAAAAAAAAAAAAAAACPLwLkfd4qzpx7aamLZiUIzUmGDs18m8n9vQQ1taMyJ%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DphYPn9kSvzKn5ckJX%252BGRAeeu0Ew%253D)